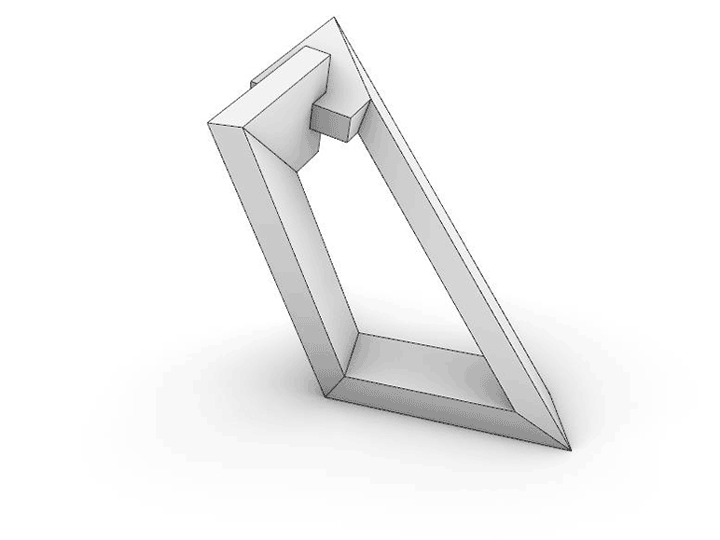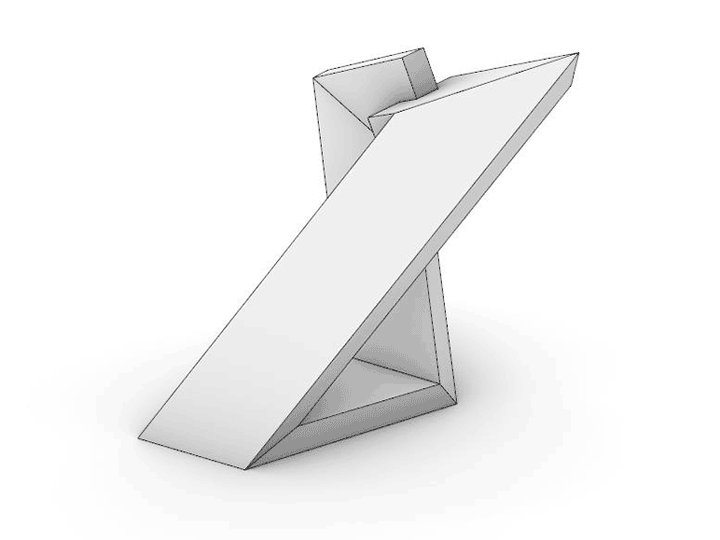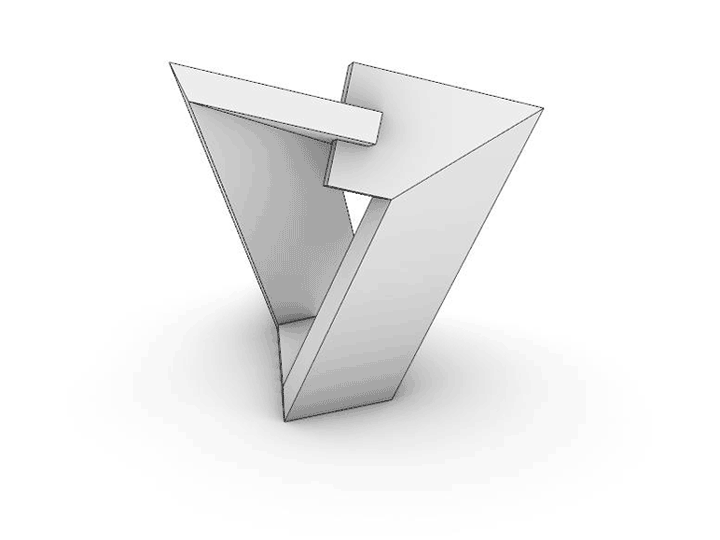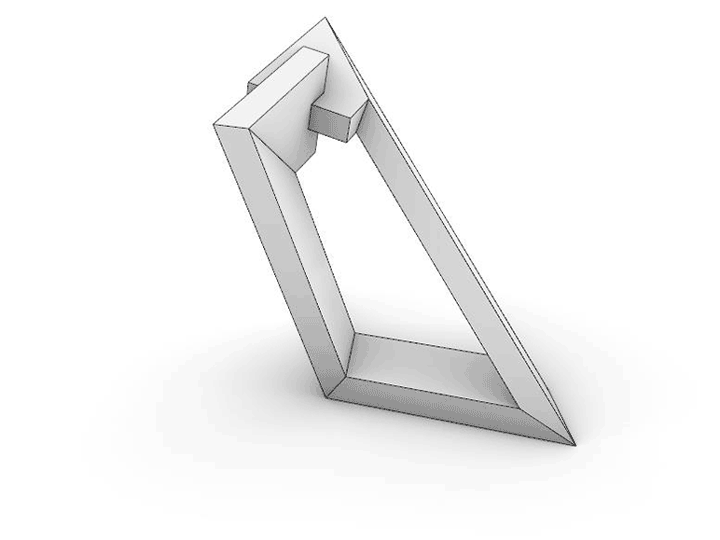
Many of the sculptures that I create are the outcome of playing a particular geometrical game. This piece began with a simple premise: working with one fixed length of rectangular tubing, would it be possible to make a series of bends that would result in the material wrapping back to itself, with the ends intersecting at exactly 90 degrees to each other? And would it be possible to do this with zero material waste?

To solve this problem, I wrote an algorithm that will geometrically construct the sculpture from four points in space. These become the center points for making diagonal cuts to construct compound miter joints (cut at two angles simultaneously). The animations illustrate how the length of tubing is cut, the parts are rotated, and then reassembled to bring the ends back together. The end components slightly overlap, for the strongest visual reading of the 90-degree relative rotation.

I designed the algorithm to allow me to measure the overall length of the tubing, the relative rotation angle between the end positions, and whether the center of gravity of the piece falls directly over the base, which will allow it to be stable and stand. Very small changes in the locations of any of the four points will significantly change these outcomes. Through a laborious process of trial and error, the points were slowly moved through space until all the goals were satisfied.

This design is only one solution out of an infinite number of other configurations that would also satisfy the design goals. Rather than search for them through a time-consuming trial and error process of manually moving points, I am next experimenting with using a genetic solver to automate the search for other solutions. Theoretically, I could have an infinite number of sculptures all constructed from the same length of tubing, that all wrap back at 90 degrees, and all look different from each other.